• About the Journal |
  • Submit a Manuscript |
  • Published Articles
  • Home |
  • Journals |
  • About Us
  • Abstracting and Indexing
  • Aims and Scope
  • Article Processing Charges
  • Author Guidelines
  • Contact Information
  • Editorial Board
  • Editorial Workflow
  • Email Alerts
  • Ethics of Publication
  • Open Access
  • Open Special Issues
  • Our Policy
  • Published Articles
  • Reviewer Guidelines
  • Subscription Information
Journal of Transition Metal Complexes
Vol. 3 (2020), Article ID 246094, 6 pages
doi:10.32371/jtmc/246094
Research Article

Calculating the Equilibrium Constants for All Monoazide Lanthanide Complexes in Aqueous Solution Based on the Formation of Eu(III)/N3−

Eliana Maria Aricó1 and Horacio Dorigan Moya2

1Instituto Federal de Ensino, Ciência e Tecnologia de São Paulo, IFSP, Campus São Paulo, Rua Pedro Vicente, 625, São Paulo, SP 09011-010, Brazil
2Faculdade de Medicina da Fundação do ABC, Centro de Estudos, Pesquisa, Prevenção e Tratamento em Saúde (CEPES), Av. Príncipe de Gales, 821, Santo André, SP 09060-650, Brazil
Address correspondence to Horacio Dorigan Moya, [email protected]

Received 10 February 2020; Revised 21 July 2020; Accepted 22 July 2020; Published 22 August 2020

  • Download PDF

How to Cite this Article

Eliana Maria Aricó and Horacio Dorigan Moya, Calculating the Equilibrium Constants for All Monoazide Lanthanide Complexes in Aqueous Solution Based on the Formation of Eu(III)/N 3 − , Journal of Transition Metal Complexes, 3 (2020), art246094. doi:10.32371/jtmc/246094

Abstract

Interest in lanthanide (Ln)/azide ( N 3 − ) chemical interactions, especially those involving Eu(III), has recently increased because N 3 − quenches the luminescence of some lanthanides. Consequently, accurate equilibrium constant values for Ln/N 3 − complexes are useful thermodynamic data. Herein, potentiometrically determined equilibrium constant data for the Eu(N3)2+ complex in aqueous solution at constant ionic strength (2.0 mol L−1, with NaClO4) and temperature (25.0 ± 0.1 °C) are reported. Data for the average number of ligands ( n ¯ ) were obtained by measuring the pH of the Eu(III)/N 3 − /HN 3 system. The relationship between the integrated n ¯ versus [ N 3 − ] curve, built by consecutively incrementing [ N 3 − ] , provided the Fronaeus function, F0(L). This relationship (in the 0.010–0.10 mol L−1 [ N 3 − ] range) at four different Eu(III) concentrations (28.6–45.2 mmol L−1) revealed a single mononuclear complex (β1 = 4.51 mol−1 L). This β1 value was used in a mathematical approach to calculate the β1 values of all other lanthanides.

Keywords

europium; azide; complex formation; stability constants; lanthanides

1. Introduction

Studies into lanthanide (Ln) azides have their origins in the last years of the nineteenth century. In 1896, Dennis was the first researcher to mention interactions between inorganic azides and lanthanides, describing the use of potassium azide (KN3) as a precipitating agent for the quantitative separation of Th(IV) from other rare earths present in monazite, a mineral found in Brazil [1]. In 1931, Ant-Wuorinen used a sodium azide (NaN3) solution to fractionally precipitate rare earths [2], and ten years later he separated rare earth alkalis by the electrolysis of their respective azides [3]. La(III) and Ce(III) were the first lanthanides to be evaluated separately in aqueous solution, and equilibrium constants of their complexes with N 3 − were determined by potentiometry [4]. Soon after, equilibrium constants for complexes formed between N 3 − and other Ln(III) ions in aqueous solution were determined. In 1975, Ezaby and Abdel-Aziz were the first to publish spectrophotometrically determined data for the azide complexes of Pr(III), Nd(III), and Sm(III) [5].

In 1977, Cuillerdier et al. determined values for Nd(III) and Er(III) complexes by spectrophotometric and potentiometric methods [6]. In the same year, Godinho et al. determined equilibrium constants for the monoazide complexes of La(III), Nd(III), and Er(III) by spectrophotometry, and reported values that were of the same order of magnitude [7]. A decade later, Choppin and Barber studied the complexations of N 3 − with lanthanide (Ln3+) and actinide (An3+) ions using solvent extraction and radioanalysis, and showed that Ln3+ monoazide complexes, particularly those of Pm(III), Eu(III), and Tm(III), are slightly less stable than the An3+ monoazide complexes of Am(III), Cm(III), and Cf(III) [8].

Musikas et al. evaluated the formation of some Ln/N 3 − complexes by solvent extraction with thenoyltrifluoroacetone and spectroscopic techniques (specifically UV, Raman, and NMR), and reported that monoazide complexes of Nd(III), Eu(III), and Yb(III) have the same equilibrium constant values. They also mentioned the formation of azido complexes containing higher numbers of N 3 − groups for the same lanthanides, namely, Nd(III), Eu(III), and Yb(III), and two actinides, namely, Am(III) and Cm(III), in highly concentrated N 3 − solutions [9].

Despite the above-mentioned studies, interactions between N 3 − and all 4f block elements in an aqueous solution have not been extensively studied to date. The currently available data are also not completely conclusive, which is ascribable to the high oxophilicity of lanthanides, resulting in an unfavourable competition between the azide ion and water, with Ln(III) ions preferring oxygen donor ligands; hence, methods using different analytical techniques are required for determining these equilibrium constant values.

Interest in chemical interactions between N 3 − and Ln(III) ions, especially Eu(III), has increased over the past few decades because N 3 − is able to quench the luminescence of some Ln(III) ions in aqueous [10,11] and nonaqueous [12] solutions. Therefore, the value of the equilibrium constant of the complex formed between Eu(III) and N 3 − obtained under careful experimental conditions and high precision is very useful thermodynamic information.

In the present study, we carefully determined the value of the formation constant, β1, for the Eu(N3)2+ monoazide complex in aqueous solution using a calibrated glass electrode, constant ionic strength, and temperature control. In addition, this β1 value was then used in a mathematical procedure to calculate the equilibrium constants of the monoazide complexes of all other 4f block elements. This approach provides a reasonable alternative method for determining values that have not yet been obtained experimentally.

2. Experimental

2.1. Materials

A Metrohm 654 pH meter and glass electrode (Metrohm AG, Herisau) combined with a Ag/AgCl reference electrode (6.0210.100) filled with 3.0 mol L−1 NaCl, was used at 25.0 ± 0.1 °C in the pH experiments in this study.

2.2. Chemicals

All reagents were of analytical-grade and were obtained from Merck, Sigma-Aldrich or Fluka Chemie A. G. Deionised water was used to prepare all solutions.

A 5.48 mol L−1 sodium perchlorate (NaClO4, 122.44 g mol−1, Merck) solution was prepared by dissolving of 671.0 g of NaClO4 in 1.0 L of water in a volumetric flask. The solution was standardised by gravimetry by taking small aliquots (2.00–3.50 mL) and drying in an oven at 120 °C to constant weight [13,14,15].

A 1.0 mol L−1 sodium hydroxide (NaOH, 40.00 g mol−1, Merck) solution and a 0.250 mol L−1 sulfuric acid (H2SO4, 98.08 g mol−1, Merck) solution were prepared and standardised as described elsewhere [16].

A 1.0 mol L−1 perchloric acid solution was prepared by dissolving HClO4 (100.46 g mol−1, d = 1.67 g mL−1, 70–72%, Merck) in water and standardising with a 1.0 mol L−1 NaOH solution.

A 4.38 mol L−1 sodium azide (NaN3, 65.01 g mol−1, Merck) solution was prepared by dissolving 284.7 g of NaN3 in 1.0 L of water in a volumetric flask. Standardisation was achieved by adding 25.0 mL of a 0.250 mol L−1 H2SO4 solution in 2.0 mL of 4.38 mol L−1 NaN3 solution, boiling to remove the volatile hydrazoic acid (HN3), followed by back titration of the remaining H2SO4 solution with a 1.0 mol L−1 NaOH solution and phenolphthalein as indicator [13,14,15].

A 0.35 mol L−1 Eu(III) perchlorate (Eu(ClO4)3) solution was prepared by directly reacting Eu(III) oxide (Eu2O3, 351.93 g mol−1, 99.9%, Sigma-Aldrich) with HClO4. Eu2O3 (∼ 3.5 g) was transferred to a 1.0 L beaker containing 500 mL water and then perchloric acid (HClO4, 100.46 g mol−1, d = 1.67 g mL−1, 70–72%, Merck) was slowly added in excess [17]. Mild heating was required to dissolve the Eu2O3. After filtering off the excess unreacted Eu2O3, the obtained solution was 10-fold concentrated by controlled evaporation (∼50 mL), after which a 1.0 mol L−1 HClO4 solution was used to adjust the pH to 2.0 in order to prevent hydrolysis [18]. Standardisation was carried out by complexometric titration with EDTA [19]. Briefly, 1.00 mL of the Eu(ClO4)3 solution was transferred to a 25-mL conical flask and hexamethylenetetramine powder was added until pH 6.0 was achieved, after which 100 mg of a xylenol orange:KNO3 mixture (1:90 w/w) was added and the solution was titrated with a 0.01 mol L−1 EDTA solution until the colour changed from purplish red to yellow.

2.3. Working solutions and strategy

Ten different N 3 − /HN 3 buffer working solutions (10.0 mL) were prepared by mixing (115–1.140 μL) of 4.38 mol L−1 NaN3 with (250–2.490 μL) of 1.0 mol L−1 HClO4. The N 3 − concentrations in these working solutions ranged between 0.010 mol L−1 and 0.10 mol L−1. The ionic strength was adjusted to 2.0 mol L−1 by adding (9.0–8.2 mL) of 5.48 mol L−1 NaClO4.

Four amounts (0.900–1.500 μL) of 0.3482 mol L−1 Eu(ClO4)3 solution were added to separate samples of each N 3 − /HN 3 buffer working solution such that the Eu(III) concentrations in the final solutions ranged from 28.6 mmol L−1 to 45.2 mmol L−1. Changes in pH were measured from the initial (pH1) to the final (pH2) value after adding the Eu(III) solution to the N 3 − /HN 3 buffers, and followed potentiometrically using a calibrated glass electrode.

2.4. Potentiometric measurements and data treatment

In order to measure the hydrogen ion concentration, a 0.05 mol L−1 potassium phthalate buffer solution (conditional pH = 3.812) with the same ionic strength as the working solutions (2.00 mol L−1, NaClO4) was used to calibrate the glass electrode [13,14,15]. This potassium phthalate solution had been previously calibrated with a 0.0100 mol L−1 HClO4 solution at the same ionic strength (2.00 mol L−1; NaClO4).

3. Results and discussion

The mass balances and the Henderson-Hasselbalch equation (1) for buffer solutions were applied to the N 3 − /HN 3 system in which N 3 − acts as both a ligand for Eu(III) and as a component of the buffer solution [13,14,15,20]. After reaching chemical equilibrium, the pH measurement provides the equilibrium concentrations, namely [ N 3 − ] 1 and [HN3]1. Subsequent addition of 0.35 mol L−1 Eu(ClO4)3 solution results in a new equilibrium condition for pH2 and, consequently, values of [ N 3 − ] 2 and [HN3]2 [13,14,15]:

pH = pK HN 3 + log [ N 3 − ] [ HN 3 ] . (1)

A conditional pKa for HN3 at an ionic strength of 2.00 mol L−1 (NaClO4) and a temperature (T) of 25.0 ± 0.1 °C were determined for each pH experiment. Determining the pKa values in different experiments has been found to be a reliable procedure as it corrects for any drift in junction potential, small losses of volatile HN3, and even possible slope deviations of the glass electrode. The mean pKa value for HN3 was determined to be 4.626 ± 0.028 under these experimental conditions.

Because the formation and stability of the Eu(III)/N 3 − complex is pH-dependent and hydrolytic species, such as Eu(OH ) 2 + , may be present in solutions at pH > 6.0 [21], the experimental approach used in the present potentiometric study is advantageous since the pH of the N 3 − /H N 3 buffer solution lies in the 4.4–4.7 range (Table 1) and such hydrolytic species are unlikely to be present.

tab1
Table 1: Calculated values of the Fronaeus function, F0(L), determined by integrating the n ¯ versus [ N 3 − ] 2 data (I = 2.00 mol L−1 (NaClO4); T = 25.0 ± 0.1 °C).

The average number of ligands, n ¯ (Bjerrum’s function) [20,22], was determined using QuickBasic 4.50 (Microsoft) (as described elsewhere [13]) by employing (2),

n ¯ = (CL−[L]) CM = [ML]+2⋅[M L2]+⋯+n⋅[M Ln] [M]+[ML]+[M L2]+⋯+[M Ln]
= β1⋅[L]+2⋅β2⋅[L]2+⋯+n⋅βn⋅[L]n 1+β1⋅[L]+β2⋅[L]2+⋯+βn⋅[L]n ,   (2)

where CL, CM, [L], [M], [ML], and β are the analytical concentration of the ligand, the analytical concentration of the cation, the equilibrium concentration of the ligand, the equilibrium concentration of the cation, the equilibrium concentration of the complex, and the stability constant [22], respectively.

An n ¯ versus [ N 3 − ] 2 curve was built by taking small and consecutive increments of [ N 3 − ] 2 [20,22]. Since the same n ¯ versus [ N 3 − ] 2 curve (Figure 1) was obtained at the four Eu(III) concentrations, CEu(III), we concluded that no polynuclear complexes are formed in the Eu(III) concentration range used (28.60–45.18 mmol L−1) in this study.

fig1
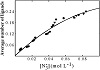
Figure 1: Curve describing the formation of the Eu(III)/N3− system (CEu(III)/mol L−1: ● = 28.60 × 10−3, ▼ = 34.32 × 10−3, ■ = 39.85 × 10−3, and ◆ = 45.18 × 10−3).

A computer program elaborated in QuickBasic 4.50 (Microsoft) [13,14,15,23] was used to integrate the n ¯ versus [ N 3 − ] 2 curve to obtain the Fronaeus function, F0(L), as shown in (3) [20]:

F 0 (L) = 1 + ∑ n = 1 n [ N 3 − ] n . (3)

Treatment of the F0(L) data using a computer method for determining equilibrium constants [13,14,15] revealed solely the formation of the Eu(III) monoazide complex (Eu(N3)2+) under these experimental conditions, with a β1 value of 4.51 ± 0.11 mol−1 L.

Table 2 lists a selection of literature-reported equilibrium constant data for monoazide lanthanide complexes, Ln(N3)2+. Most of these values were determined by spectrophotometry or potentiometry, which are very useful techniques for this purpose. Table 2 reveals that most equilibrium constants are of the same order of magnitude. The equilibrium constants for Pr(III), Nd(III), and Sm(III) with N 3 − obtained using the Scott and dilution methods [5] are in good agreement; however, these low values do not agree with those obtained by other authors, and these differences cannot be attributed solely to the absence of temperature control in these experiments. In the study reported by El Ezaby and Abdel-Aziz [5], two absorbent species were found in solution; one was assumed to be Ln(III), with the other the corresponding azide complex. These two species were determined only by graphical methods, and the calculational methods (Scott’s equation and dilution) were used with some modifications to suit conditions under which Ln(III) ions and their complexes absorb at the same wavelength, which may provide reasons for the low equilibrium constant values obtained.

tab2
Table 2: Selected equilibrium constants, β1, for the monoazide complexes of lanthanides.

Kumok and Serebrennikov [24] statistically evaluated the global equilibrium constants, β1, of rare-earth, except Pm(III), monocomplexes with 55 different ligands, and found that the logarithms of the β1 values were linearly correlated. According to these authors, the β1 value of any lanthanide monocomplex (LnL) is related to that of the lanthanum monocomplex (LaL) through (4). In this equation, a and b are constants obtained by statistically treating each trivalent Ln cation, and logβ1(LnL) and logβ1(LaL) refer to the monocomplexes of the lanthanide (Ln) and lanthanum (La), respectively,

log β 1 (LnL) = a × log β 1 (LaL) + b . (4)

The a and b values for Eu(III) are 1.1367 and 0.009, respectively [24]. With this in mind, we applied (4) to the β1 value found in the present study for Eu(N3)2+ (i.e., 4.51 mol−1 L), which provided 3.70 mol−1 L as the β1 value for La(N3)2+. Since the values of a and b for trivalent Ln cations have been reported [24], the β1 values were calculated for the monoazide complexes of all lanthanides, the results of which are listed in Table 2.

As expected, these complexes are very weakly bound since trivalent lanthanides are hard cations [25] and prefer to form complexes with oxygen or mixed oxygen-nitrogen donor ligands rather than nitrogen donors such as N 3 − . Despite being weak, the equilibrium constants calculated using only the equation developed by Kumok and Serebrennikov [24] for the Ln monocomplexes with N 3 − also need to be determined experimentally. The values obtained experimentally will facilitate a more realistic interpretation of the calculational methodology used in the present study for determining these same values mathematically.

4. Conclusion

Potentiometric measurements using a calibrated glass electrode at constant ionic strength (2.0 mol L−1; NaClO4) and controlled temperature (T = 25.0 °C) enabled the accurate determination of the formation constant for the Eu(N3)2+ complex in aqueous solution (β1 = 4.51 ± 0.11 mol−1 L). No polynuclear complex is formed in the Eu(III) concentration range used in this study (28.60–45.18 mmol L−1). The β1 value found for the Eu(N3)2+ complex was used in a mathematical approach to calculate the β1 values for the monoazide complexes of all other 4f block elements, which provides a reasonable alternative procedure for determining values that have not yet been obtained experimentally.

Acknowledgments

The authors acknowledge financial support from the following Brazilian agencies: Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) and Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq). This study is dedicated to Professor Eduardo Fausto de Almeida Neves (1933–2006).

Conflict of interest

The authors declare that they have no conflict of interest.

References

  1. L. M. Dennis, The separation of thorium from the other rare earths by means of potassium trinitride, J Am Chem Soc, 18 (1896), 947–952.
  2. J. Ant-Wuorinen, The separation of the rare earth alkalies by hydrolysis of their azides, Teknillinen Aikakauslehti, 21 (1931), 365–369.
  3. J. Ant-Wuorinen, The separation of the rare earths by electrolysis of their azides, Suomen Kemistilehti B, 13 (1940), 1–3.
  4. F. Maggio, L. Pellerito, V. Romano, and T. Pizzino, Complex formation equilibriums between lanthanum(III), cerium(III), and azide ions, Atti della Accademia di Scienze, Lettere e Arti di Palermo, Part 1: Scienze, 33 (1974), 195–201.
  5. M. S. El Ezaby and I. E. Abel-Aziz, Interaction of azide ions with some light lanthanides, J Inorg Nucl Chem, 37 (1975), 2013–2016.
  6. C. Cuillerdier, C. Musikas, and M. Marteau, Pseudohalide complexes of 4f and 5f elements, in Meeting on Actinides (Paris, France), 1977.
  7. O. E. S. Godinho, L. M. Aleixo, E. Stein, and N. M. S. de Vasconcelos, Study of the azide complexes of La(III), Nd(III) and Er(III) in aqueous solution, An Acad Bras Cienc, 54 (1982), 97–98.
  8. G. R. Choppin and D. W. Barber, Azide complexes of LnIII and AnIII, J Less Common Met, 149 (1989), 231–235.
  9. C. Musikas, C. Cuillerdier, J. Livet, A. Forchioni, and C. Chachaty, Azide interaction with 4f and 5f ions in aqueous solutions. 1. Trivalent ions, Inorg Chem, 22 (1983), 2513–2518.
  10. S. Lis, T. Kimura, and Z. Yoshida, Luminescence lifetime of lanthanide (III) ions in aqueous solution containing azide ion, J Alloys Compd, 323 (2001), 125–127.
  11. S. Lis, Luminescence spectroscopy of lanthanide (III) ions in solution, J Alloys Compd, 341 (2002), 45–50.
  12. S. Lis, T. Kimura, Z. Yoshida, and S. But, Luminescence study of lanthanide (III) ions in non-aqueous solutions containing azide ions, J Alloys Compd, 380 (2004), 173–176.
  13. H. D. Moya, E. A. Neves, M. E. Vázquez Suárez-Iha, and N. Coichev, Study of complex formation in the manganese(II)/azide system, Talanta, 43 (1996), 67–72.
  14. H. D. Moya, E. A. Neves, and N. Coichev, The stabilization of managese (III) by azide ions in aqueous solution, Talanta, 44 (1997), 797–803.
  15. H. M. S. Leite, H. D. Moya, N. Coichev, and E. A. Neves, The interaction of 2-amino-2-hydroxymethyl-1,3-propanediol with cobalt(II) and manganese(II) ions, J Coord Chem, 49 (2000), 251–259.
  16. G. H. Jeffery, J. Basse, J. L. Mendham, and R. C. Denney, Vogel’s Textbook of Quantitative Chemical Analysis, Longman Group, London, 5th ed., 1989.
  17. M. E. Brotto and T. Rabockai, Chronopotentiometric investigation of the Eu(III)/Eu(II) system in propionic acid media, Lanthanide and Actinide Research, 3 (1989), 151–162.
  18. D. D. Perrin, Ionisation Constants of Inorganic Acids and Bases in Aqueous Solution, Pergamon Press, Oxford, 1982.
  19. E. Merck, ed., Métodos complexométricos de valoración con Titriplex, Merck, Darmstadt, Germany, 3rd ed., 1972.
  20. M. T. Beck, Chemistry of Complex Equilibria, Van Nostrand, London, 1970.
  21. C. F. Baes and R. E. Mesmer, The Hydrolysis of Cation, John Wiley & Sons, New York, 1976.
  22. H. Rossotti, The Study of Ionic Equilibria: An Introduction, Longman Publishing Group, New York, 1978.
  23. E. F. A. Neves, I. G. R. Gutz, and R. G. Tavares, Calculation of stability constants from potentiometric data by desk computers. A simplified approach, J Electroanal Chem Interf Electrochem, 179 (1984), 91–98.
  24. V. N. Kumok and V. V. Serebrennikov, Stability of rare-earth complexes, Russ J Inorg Chem, 10 (1965), 1095–1098.
  25. S. F. A. Kettle, Physical Inorganic Chemistry: A Coordination Chemistry Approach, Oxford University Press, Oxford, 1998.

Copyright © 2020 Eliana Maria Aricó and Horacio Dorigan Moya. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.